Wanna bet?

We’re talking about probability, so let’s start with a game. I’ve got a six-sided die with five different numbers on the sides. One number appears twice. You, the player, have to guess which number appears twice. I’ll give away the answer so this will be easier to visualize:

1 – 2 – 3 – 4 – 5 – 5

If a correct guess pays $1, an uninformed guess is worth 1/5 of a dollar, or 20 cents. But I offer you a better chance than this. I will let you roll the die a few times before guessing.

The strategy here is obvious: watch the rolls and guess the number that appears the most times. If there’s a tie, pick randomly from the winners. Here’s the effect:

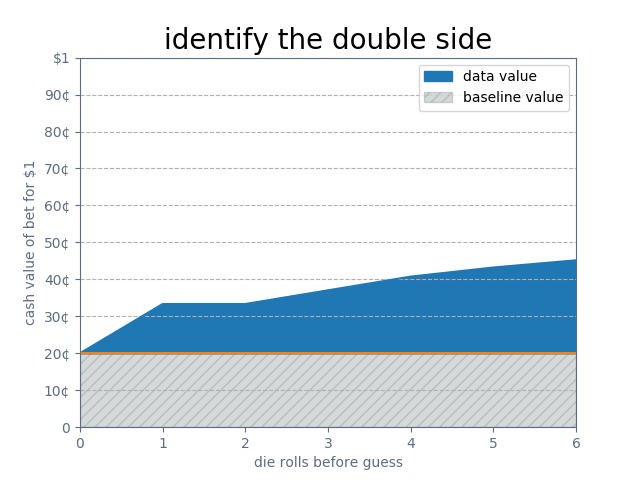
That’s a lot of effect! As you can see, the value of your bet more than doubles after observing four rolls of my die.

But you can do much better than that. If you bet every round, I will have to tell you if you won or lost. You will then have two pieces of data: 1) the rolls on the die, and 2) one die eliminated for every wrong guess.

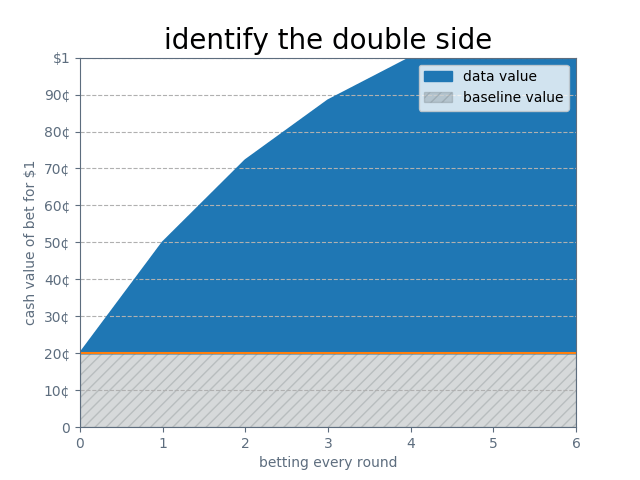
Combining these two information streams, you will have a 50% chance to win after just two guesses! (one guess before the first round, then one guess after)

How about some real stakes?

After witnessing the predictive power of these die rolls, you may be anxious to apply this power to something more important than a $1 bet.

So, here’s the new game. You have five warehouses and one fireman. One of the warehouses is twice as likely to catch on fire as any one of the other four. These are the same odds as our die game. Your job is to predict the next fire, and move the fireman to the correct warehouse.

The strategy, again, is simple: treat every fire as a die roll. Assume whatever warehouse burns the most times is the most flammable warehouse (move the fireman there). In case of a tie, choose randomly from the winners.

Let’s see how you do.

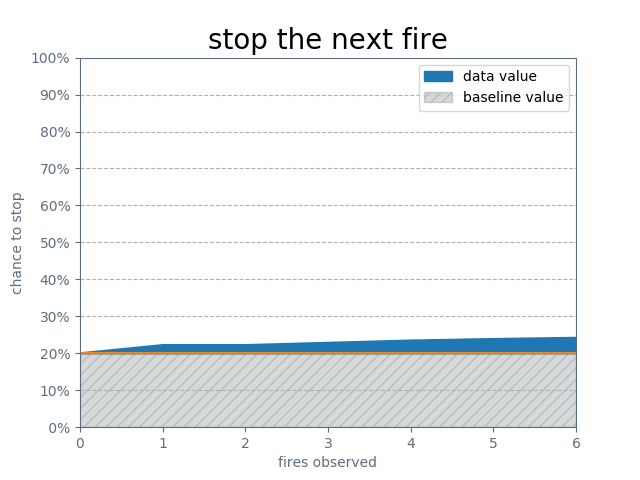
Doesn’t look so good. What happened?

The most flammable warehouse will only catch on fire 1/3 of the time. Even when you’re right (even when you correctly guess the most flammable warehouse), you’re probably still wrong (about where the next fire will occur)! A correct guess will never be confirmed. Even when you do stop a fire, you may still have your fireman at the “wrong” warehouse.

Your effect will increase with more data, but will never surpass the effect of a second fireman, even if you count a million fires.

And you’ll never have more data anyway. That’s another difference between games and real life: in life, the answers change. You will buy and sell warehouses, warehouses will change management, individual warehouses will become more and less flammable over time.

But you can see some effect from tracking fires and moving your fireman around. Prediction is hard, but maybe you’re not wandering around in complete darkness.

Hey, let’s run around in complete darkness for a minute.

We’ve seen here that even large game effects are reduced (objectively) to something almost indistinguishable from noise in real life.

To close, I’ll compare this diminished game effect to a native real-life effect. In real life, we don’t know exactly how flammable our most flammable warehouse is. In fact, it would take us quite a few fires to realize that one warehouse is indeed more flammable than the others. In real life, we buy as much protection as we can afford and hope for the best.

Let’s assume we can’t afford another full-time fireman, but we have found a part-time fireman who will show up once every 10 days. Here are the compared effects:

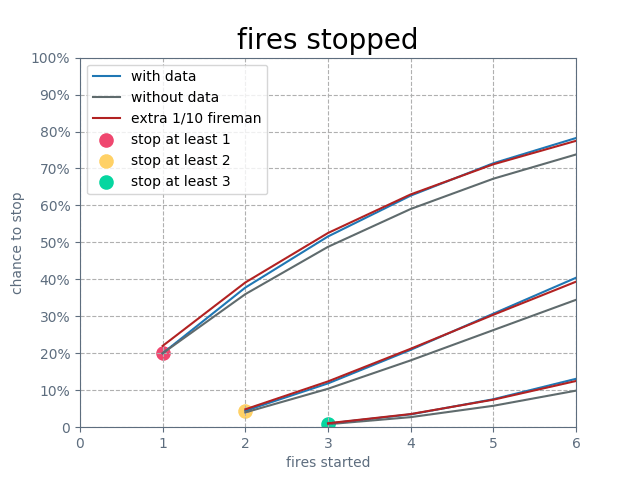
The takeaway? An “educated guess” is still a guess. Buy it if it’s very cheap, but even then consider some form of insurance instead.