The problem:

Generalization:

In it’s simplest form:

This is meant to be a solution at a middle-school reading level (starts just after add, subtract, multiply, and divide). In 4 languages: English, “Math”, Python 3, and Haskell.

Coders will identify optimizations everywhere, I’ve tried to keep the code explanations as close as possible to the English-language explanations–no skipped (“optimized away”) steps or hidden algebra.

first, forget about the grid

The combinations we’re counting are the combinations that can show on an odometer, or a wheel-style combination lock. These are different than combinations drawn from a bag or a deck of cards. Odometers and wheel-style combination locks count the way (natural) numbers do. Every possible combination (dart-throwing result) in NNT’s dart problem can be expressed on a wheel-style combination lock with “number of darts” wheels, each wheel with “number of boxes” symbols. Don’t get thrown off by the “2D grid” of boxes.

count all the combinations

This is the easiest part, and gives us an idea how to count the smaller sets of combinations. Our problem is 8 darts thrown at 16 boxes. We’ll solve that later on, first let’s look at 3 darts thrown at 4 boxes..

English

1. There are 4 possible positions for the first dart.

2. For each of those 4 positions for the first dart, there are 4 possible positions for the second dart.
   That’s \({\textstyle 4 * 4 = 16}\) combinations for the first two darts.

3. For each of the 16 possible combinations of the first two darts, there are 4 possible positions for the third dart.
   That’s \(4 * 4 * 4 = 64\) combinations for all three darts.

Let’s have a look at all 64 of them, so we can see that they count exactly like numbers.

Math

—our puzzle—

Python

>>> 16 ** 8
4294967296

Haskell

Prelude> 2 ^ 5
32

list the groupings

Counting all of the possible sequences was easy enough. Now we just have to count the sequences we want, then divide that by the count of all sequences.

The sequences we want are any sequences with 3 or more darts in any one box. Those groupings are easy to pick out once we list all possible groupings.

English

“Integer Partition” is the name for the list of ways you can add integers to create a given total. This one may be clearer with an image. In the image below, each column is the integer partition for the number at the top of the column.

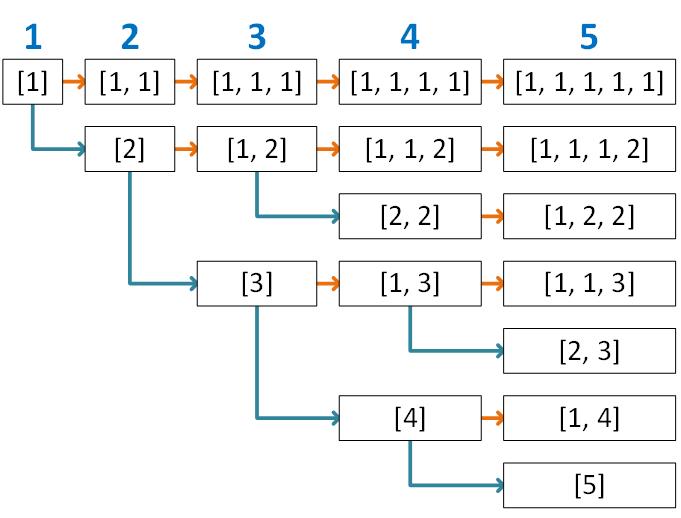
As you can see, each block in column 1 adds up to 1, each block in column 2 adds up to 2, etc.

The arrows in the picture show how these partitions are put together:

• orange arrow: for each block in the previous column, add [1] to the front. So [3] becomes [1, 3]

• teal arrow: for each block in the previous column. If that block is one number long (e.g., [3]) or if the first number in the block is less than the second number (e.g., [1, 2]), add 1 to the first number. So [3] becomes [4] and [1, 2] becomes [2, 2].

Imagine each of these partitions as a group of darts. A few of the partitions of 8 (our number of darts) are

• 1+1+1+1+1+1+1+1 (one dart each in eight different squares)

• 8 (all darts in one square)

• 4+3+1 (four darts in one square, three darts in another, and one dart in a third)

Math

\(\mathcal{P}(n) =\) the integer partitions of \(n\)

Python

def partitions(n):
 """Integer partitions

 Start with the partition of 1 and keep updating until you
 reach the partition of :n:.
 """
 current = [[1]]
 while current[-1] != [n]:
 next_partition = []
 for p in current:
 # orange arrow
 next_partition.append([1] + p)
 # teal arrow
 if len(p) == 1 or p[0] < p[1]:
 next_partition.append([p[0] + 1] + p[1:])
 current = next_partition
 return current

>>> partitions(8)
 [
 [1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 2],
 [1, 1, 1, 1, 2, 2], [1, 1, 2, 2, 2], [2, 2, 2, 2],
 [1, 1, 1, 1, 1, 3], [1, 1, 1, 2, 3], [1, 2, 2, 3],
 [1, 1, 3, 3], [2, 3, 3], [1, 1, 1, 1, 4], [1, 1, 2, 4],
 [2, 2, 4], [1, 3, 4], [4, 4], [1, 1, 1, 5], [1, 2, 5],
 [3, 5], [1, 1, 6], [2, 6], [1, 7], [8]
 ]

Haskell

-- integer partitions
partitions :: Integral p => p -> [[p]]
partitions n = nextPartition [[1]]
 where
 -- orange arrow
 oneAdded = map (\xs -> 1:xs)
 -- teal arrow
 headIncd ps = [x+1:xs | x:xs <- ps, null xs || x < xs !! 0]
 nextPartition ps
 | last ps == [n] = ps
 | otherwise = nextPartition $ oneAdded ps ++ headIncd ps

factorial

We counted combinations above with

every choice * every choice * every choice

That works when the choices can repeat. Factorial counts how many ways you can line up a group of individual items (no repeats), so factorial looks like

every choice * every choice except the first one * every choice except the first two

English

1. Four items to choose for the first spot, so 4 possible arrangements for the first spot.

2. Three items left to choose for the second spot, so 4 * 3 = 12 arrangements for the first two spots.

3. Two items left to choose for the third spot, so 4 * 3 * 2 = 24 arrangements for the first three spots.

4. One item left for the fourth spot, so 4 * 3 * 2 * 1 = 24 arrangement for all four items.

Here they are.

Math

Python

def factorial(n):
 """How many ways can :n: items be lined up?"""
 total = 1
 for i in range(2, n + 1):
 total *= i
 return total

>>> factorial(8)
40320

Haskell

-- factorial
factorial :: (Num a, Enum a) => a -> a
factorial n = product [1..n]

arranging items that might match

\(x^n\) works for counting sequences with repetition.

\(x!\) works for counting sequences without repetition.

What do we do when items can repeat sometimes?

Here is another arrangement of four items, but this time, they’re not all distinct. Instead of arranging 0-1-2-3, we’re arranging 0-0-1-2. This creates a lot of duplicate arrangements. I’ve grayed out the duplicates.

English

It doesn’t matter what order the duplicates are in (“00” == “00”).

1. Arrange all of the items as if they’re distinct.

2. Divide by the arrangements of the duplicate items.

Math

Python

def arrangements(partition):
 """How many ways can multiple groups of like items be lined up?"""
 denominator = 1
 for summand in partition:
 denominator *= factorial(summand)
 return factorial(sum(partition)) // denominator

>>> arrangements([2, 1, 1])
12
>>> arrangements([3, 2, 5])
2520

Haskell

-- count arrangements with (potentially) matching items
arrangements :: Integral a => [a] -> a
arrangements xs = factorial (sum xs) `div`
 product (map factorial xs)

caution with duplicates!

Two green marbles and one red marble can be lined up three ways.

Two red marbles and one green marble can be lined up another three ways.

However, two green marbles and two red marbles line up exactly the same as two red marbles and two green marbles.

And, of course, one red marble and one green marble line up the same ways as one green marble and one red marble. This becomes important when we count multiple groups of the same size.

To count the combinations where two numbers appear three times each and three numbers appear one time each, we’ll have to make sure we don’t count three 0s and three 1s twice (or one 2, one 3, and one 4 \(3! = 6\) times).

English

1. Count the arrangements of all boxes (that will be the length of the partition.).

2. Group the boxes by hits.

3. Divide by the size of each group.

The partition describing 000111234 would be [1, 1, 1, 3, 3]. That’s 5 boxes, 3 boxes hit one time each and 2 boxes hit three times each.

1. Count the arrangements of all 5 boxes. That’s 5! = 120.

2. Group the boxes by hits. That’s three 1s and two 3s.

3. Divide by the size of each group.

4. 120 / 3! for the the 1s gives 20.

5. 20 / 2! for the two 3s gives 10.

Math

Here’s what we just counted. Each of the 10 selections below can be arranged 10,080 ways, but no selection will share an arrangement with any other.

Python

def same_size_groups(partition):
 """Frequency of partition elements."""
 return [partition.count(x) for x in set(partition)]

>>> same_size_groups([3, 3, 1, 1, 1])
[2, 3]

def selections(partition):
 """How many ordered lists with (p in partition)-sized groups?"""
 denominator = 1
 for member_count in same_size_groups(partition):
 denominator *= factorial(member_count)
 return factorial(len(partition)) // denominator

>>> selections([3, 3, 1, 1, 1])
10
>>> selections([2, 2, 2, 2])
1

Haskell

-- run lengths
sameSizeGroups :: Eq a => [a] -> [Int]
sameSizeGroups [] = []
sameSizeGroups (x:xs) = [length (takeWhile (==x) xs) + 1] ++
 sameSizeGroups (dropWhile (==x) xs)

Prelude> sameSizeGroups [1, 1, 1, 1, 2, 2, 2, 4, 4]
[4, 3, 2]

-- count ordered lists with (p in ps)-sized groups
selections :: Eq a => [a] -> Int
selections ps = factorial (length ps) `div`
 product (map factorial $ sameSizeGroups ps)

Don’t miss this!

Function “selections” is similar to function “arrangements”, but the results are not yet arranged! To get all the arrangements of

• three of one color

• three of another color

• one of a third color

• one of a fourth color

• one of a fifth color

you would need to call

selections([3, 3, 1, 1, 1]) * arrangements([3, 3, 1, 1, 1])

the groups we haven’t been counting

So far, our arrangements have been made from all of our available items. To solve the dart puzzle, we’ll need to count arrangements from only some of our items.

This part is easy, just fill in our partition with a count (0) for all the boxes we missed.

English

1. Add [0] for each missed box to your partition.

2. Count the arrangements of all boxes (that will be the length of the updated partition).

3. Group the boxes by hits.

4. Divide by the size of each group. (or skip steps 2-3 and call our above function “selections” with the updated partition.)

Working through 5 boxes with partition [1, 1, 2]:

1. Add two 0s for the boxes we didn’t hit. That gives us [1, 1, 2, 0, 0].

2. Count the arrangements of all 5 boxes. That’s 5! = 120.

3. Group the boxes by hits. That’s two 1s, one 2, and two 0s.

4. Divide by the size of each group.

• 120 / 2! for the two 1s gives 60.

• 60 / 1! for the one 2 is still 60.

• 60 / 2! for the two 0s gives us 30.

Math

\(let\ {d \in \mathbb{N} =}\) available choices (boxes).

Python

def subselections(choices, partition):
 """Count ordered lists of :choices: items
 with (p in partition)-sized groups.
 """
 unused = choices - len(partition)
 return selections(list(partition) + [0] * unused)

>>> subselections(5, [1, 1, 2])
30

Haskell

-- count ordered lists of :c: items
-- with (p in ps)-sized groups.
subselections :: (Eq a, Num a) => Int -> [a] -> Int
subselections c ps = selections $ ps ++ take (c - length ps) (repeat 0)

the full solution

There are 22 partitions of 8 darts. To answer NNT’s puzzle, we just need to count how many times each partition with a group equal to or larger than 3 appears, then divide that by the total number of combinations.

English

Working through 4 darts thrown at 6 boxes, looking for the chance of at least 3 hits in one box.

• Select the integer partitions of [4 darts] with at least [3 hits] in one group. (This is the only new step.)

• For each partition:

  • subselection-a. Add 0s to extend the partition to [6 boxes] long.
  \[[1, 3]\to[1, 3, 0, 0, 0, 0]\]
  \[[4]\to[4, 0, 0, 0, 0, 0]\]
  • subselection-b. Group the numbers in the extended partition by how many times they occur (i.e., the number of 0s, the number of 1s, the number of 2s, etc. )
  \[[1, 3] \to [\underbrace{1,}_1 \underbrace{3,}_1 \underbrace{0, 0, 0, 0}_4] \to [1, 1, 4]\]
  \[[4] \to [\underbrace{4,}_1 \underbrace{0, 0, 0, 0, 0}_5] \to [1, 5]\]
  • subselection-c. Divide the combinations (factorial) of [6 boxes] by the factorial of occurrences of each number in the partition.
  \[[1, 3]\to6!/(1!1!4!)=30\]
  \[[4]\to6!/(1!5!)=6\]
  • arrangement-a. Multiply this number by [4 darts] factorial.
  \[[1,3] \to 30 * 4! = 720\]
  \[[4] \to 6 * 4! = 144\]
  • arrangement-b. Divide by the factorial of each number in the partition.
  \[[1, 3] \to 720 / (1!3!) = 120\]
  \[[4] \to 144 / 4! = 6\]

• Add up the results for all selected partitions.

• Divide by total number of partitions ([6 boxes] ^ [4 darts])

Math

\(let\ {n \in \mathbb{N} =}\) number of darts

\(let\ {d \in \mathbb{N} =}\) number of boxes

\(let\ {m \in \mathbb{N} =}\) minimum cluster size we’re searching for

\(let\ {P \in [\mathcal{P}(n) : max \geq m] =}\) partitions with at least m-sized groups

Python

def darts(n, d, m):
 """You throw n darts uniformly randomly on a map with d squares.
 What's the probability of getting m darts in a single square
 (any square)?
 """
 qualified = [p for p in partitions(n) if max(p) >= m]
 m_size_groups = sum(subselections(d, p) * arrangements(p) for p in qualified)
 return m_size_groups / d ** n

>>> darts(5, 17, 3)
0.03162078998096287
>>> darts(4, 7, 2)
0.6501457725947521
>>> darts(8, 16, 3)
"I won't give it away. Have fun."

Haskell

-- throw n darts uniformly randomly on a map with d squares.
-- probability of getting m darts in a single square (any square)?
darts :: Int -> Int -> Int -> Ratio Int
darts n d m = mSizeGroups % (d ^ n)
 where
 qualified = [p | p <- partitions n, maximum p >= m]
 mSizeGroups = sum [subselections d q * arrangements q | q <- qualified]

Prelude> darts 5 17 3
2641 % 83521
Prelude> realToFrac $ darts 5 17 3
3.162078998096287e-2

throw more darts!

What extra steps are required when you throw more darts than you have boxes? Here are a few answers so you can check your work.

n=12 darts, d=2 boxes, m=6 grouped →

n=14 darts, d=3 boxes, m=8 grouped →

n=12 darts, d=11 boxes, m=4 grouped →